Oι πύλες προς το Σύμπαν είναι ανοικτές. Η Οδύσσεια του Διαστήματος εν εξελίξει και με δεδομένη αφετηρία ψάχνει προορισμούς και τρόπους μετάβασης. Οι σύγχρονοι «θαλασσοπόροι» -σχεδιαστές αποστολών-, αναζητούν φυσικά το κατάλληλο «ιστιοφόρο» για να εξερευνήσουν τον Ωκεανό του Σύμπαντος. Και παράλληλα προσπαθούν να χαράξουν τα -στο μέτρο του δυνατού- ιδανικά Κοσμικά Κανάλια για το ταξίδι τους, αρχής γενομένης από την «γειτονιά» της Γης, το Ηλιακό μας Σύστημα.
Το ερώτημα που αναδύεται άμεσα στην βάση αυτής της προσπάθειας είναι φυσικά το εξής:
«Υπάρχει τρόπος να περιδιαβούμε τον Διαπλανητικό Χώρο, με το δυνατόν χαμηλότερο ενεργειακό κόστος;»
Ή...
...αν υποθέσουμε ότι οι σύντροφοι του Οδυσσέα είναι η πολύτιμη ενέργεια και η Σκύλλα και η Χάρυβδη η ενεργοβόρα πλανητική βαρύτητα που κυριαρχεί στον μεσοπλανητικό χώρο, θα μπορούσαμε να βρούμε τον τρόπο να τις χρησιμοποιήσουμε προς όφελός μας, ελαχιστοποιώντας τις ενεργειακές απώλειες;
Τα όπλα στην φαρέτρα των σχεδιαστών διαστημικών αποστολών, ως προς αυτήν την παράμετρο, χρησιμοποιούν ένα -εκ πρώτης όψεως- παράδοξο πυρομαχικό: την ίδια την βαρύτητα.
Η έρευνα έχει αποδώσει καρπούς κι έχει οδηγήσει στην δημιουργία ενός μεγάλου δικτύου μεσοπλανητικών τροχιών χαμηλής ενέργειας που κάνει χρήση τόσο του φαινομένου της Βαρυτικής Σφενδόνης (τίτλος ολίγον ατυχής), όσο και των ιδιοτήτων των χαρακτηριστικών Λαγκρανζιανών Σημείων που αντιστοιχούν σε κάθε ζεύγος αλληλεπιδρώντων ουρανίων σωμάτων.
Ας πάρουμε όμως τα πράγματα με τη σειρά κι ας δούμε πρώτα πώς ακριβώς δουλεύει η Βαρυτική Σφενδόνη.
Βαρυτική Σφενδόνη ή Βαρυτική Ώθηση
Oι περισσότερες διαστημικές αποστολές που έχουν ξεκινήσει από τον πλανήτη μας για να εξερευνήσουν τον χώρο που μας περιβάλλει, από την κοντινή μας γειτονιά ως τα όρια του Ηλιακού συστήματος, είναι σχεδιασμένες με βάση την Ουράνια Μηχανική των Johannes Kepler (1571 - 1630) και Sir Isaac Newton (1643 - 1727).Σε αυτό το θεωρητικό πλαίσιο, αναζητήθηκε ένας εύκολος τρόπος χάραξης τροχιών χαμηλής ενέργειας. Οι ελιγμοί βαρυτικής ώθησης (ή όπως αλλιώς αναφέρονται οι βαρυτικές σφεντόνες), είναι ένας σχετικά απλός και ανέξοδος τρόπος να χρησιμοποιηθεί η βαρύτητα ενός μεγάλου ουράνιου σώματος για την επιτάχυνση ενός διαστημοπλοίου.
Ας παρακολουθήσουμε, λοιπόν, ένα διαστημόπλοιο που πλησιάζει έναν πλανήτη, εισερχόμενο στο βαρυτικό του πεδίο, έτσι ώστε να περάσει αρκετά κοντά του, χωρίς όμως να παγιδευτεί από αυτόν, εξερχόμενο στο τέλος από το βαρυτικό του πεδίο.
Παρατηρώντας το διαστημόπλοιο από το σύστημα αναφοράς του πλανήτη, κι εφαρμόζοντας την Αρχή Διατήρησης της Ενέργειας, οδηγούμαστε στο συμπέρασμα πως δεν αποκομίζει κανένα ενεργειακό πλεόνασμα, αφού η βαρύτητα είναι δύναμη διατηρητική. Πιο συγκεκριμένα, όσο πλησιάζει προς τον πλανήτη τόσο πιο γρήγορα κινείται, αφού η βαρυτική έλξη του πλανήτη το επιταχύνει. Καθώς όμως απομακρύνεται, η ίδια βαρυτική έλξη το επιβραδύνει, έχοντας εκ πρώτης όψεως κερδίσει μόνο την αλλαγή κατεύθυνσής του. Η περίπτωση αυτή, μοιάζει με εκείνην ενός ποδηλάτη που κατηφορίζει επιταχυνόμενος προς μία κοιλάδα ενώ στη συνέχεια επιβραδύνεται ανερχόμενος από αυτήν.
Οι παρατηρήσεις και τα συμπεράσματά μας είναι βέβαια σωστά, εφόσον βρισκόμαστε στο σύστημα αναφοράς του πλανήτη, για το οποίο ο πλανήτης είναι ακίνητος.
Δισδιάστατη απεικόνιση της κίνησης διαστημοπλοίου που
περνάει πλησίον του πλανήτη Δία, όπως φαίνεται από το
σύστημα αναφοράς του ίδιου του πλανήτη. Η ελκτική δύναμη του
Δία έχει προκαλέσει μια αξιοσημείωτη μεταβολή
στην κατεύθυνση της ταχύτητας ενώ το μέτρο της
παραμένει αμετάβλητο (VOUT=VIN).
Για έναν παρατηρητή που βρίσκεται στον ήλιο, τα πράγματα θα είναι διαφορετικά. Σύμφωνα με τον παρατηρητή αυτόν, ο πλανήτης κινείται και αυτή ακριβώς η κίνηση είναι το κλειδί για την κατανόηση του φαινομένου της βαρυτικής σφενδόνης. Στη νέα αυτή θεώρηση των πραγμάτων, πρέπει να ληφθεί υπόψιν η περιφορά του πλανήτη γύρω από τον ήλιο και η τεράστια στροφορμή του.
Καθώς το σύστημα διαστημόπλοιο - πλανήτης αλληλεπιδρά, ο πλανήτης «παρασύρει» στην κίνησή του το διαστημόπλοιο, έτσι ώστε αυτό να «κερδίζει» ένα μέρος από την στροφορμή και την κινητική ενέργεια του πλανήτη, αμελητέα για τον ίδιο, ιδιαίτερα σημαντική για το διαστημόπλοιο, αφού μπορεί να αυξήσει την ταχύτητά του έως και δύο φορές την τροχιακή ταχύτητα του πλανήτη!
Στην εικόνα που ακολουθεί, απεικονίζεται η βαρυτική ώθηση του Δία σε ένα διαστημικό σκάφος που εισέρχεται στο βαρυτικό του πεδίο.
Η ταχύτητα του πλανήτη καθώς περιφέρεται γύρω
από τον Ήλιο παριστάνεται με ένα ροζ βέλος
(απλουστευμένα φυσικά, αφού ως γνωστόν
ο πλανήτης κινείται κατά μήκος τόξου και όχι
ευθείας γραμμής. Ο ήλιος βρίσκεται στο κάτω μέρος
του διαγράμματος). Η αρχική ταχύτητα του διαστημοπλοίου
στο σύστημα αναφοράς του ήλιου, βρίσκεται αν
προσθέσουμε διανυσματικά την αρχική του ταχύτητα,
ως προς το σύστημα του πλανήτη, με την ταχύτητα
του πλανήτη, ως προς το ίδιο σύστημα. Αντίστοιχα βρίσκουμε
και την τελική ταχύτητα του διαστημοπλοίου.
Ας απλουστεύσουμε λίγο τα πράγματα, ώστε να εξάγουμε ένα μέτρο της ώθησης που ένας πλανήτης προσφέρει σε ένα διαστημόπλοιο.
. Κατά την αλληλεπίδραση των δύο σωμάτων ο πλανήτης μεταβάλλει σημαντικά την ταχύτητα του διαστημοπλοίου, χωρίς να υπάρχει μετρήσιμη μεταβολή στην δική του ταχύτητα.
. Η βαρυτική έλξη απλά στρέφει το διάνυσμα της ταχύτητας του διαστημοπλοίου, στο σύστημα αναφοράς του πλανήτη, αφήνοντας το μέγεθός του αναλλοίωτο. Αυτή ακριβώς η στρέψη (επιτάχυνση) αλλάζει το μέτρο της ταχύτητας στο ηλιοκεντρικό σύστημα αναφοράς.
Μετωπική αλληλεπίδραση
Ξεκινάμε με την απλή περίπτωση που ένα διαστημόπλοιο πλησιάζει«μετωπικά» τον πλανήτη, δηλαδή με αρχική ταχύτητα
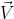παράλληλη προς την τροχιακή ταχύτητα 
του πλανήτη, έτσι ώστε να περάσει πίσω από τον πλανήτη σε μια εξαιρετικά έκκεντρη υπερβολική τροχιά και να στραφεί κατά 180o, όπως φαίνεται στην παρακάτω εικόνα. Και οι δυο ταχύτητες ορίζονται στο σύστημα αναφοράς του Ήλιου. Συμβολίζουμε 
και 
.
H μετωπική προσέγγιση του διαστημοπλοίου στον πλανήτη
μοιάζει με την ανάκρουση ενός μικρού σφαιριδίου
μπιλιάρδου από μία πολύ μεγαλύτερη σφαίρα.
Η διατήρηση της κινητικής ενέργειας και της ορμής δίνουν:
Όπου Μ, η μάζα του πλανήτη,
m, η μάζα του διαστημοπλοίου,
και οι δείκτες ΙN και OUT, αντιστοιχούν στην προ και μετάαλληλεπίδρασης κατάσταση αντίστοιχα.
Σε συμφωνία με τις παραδοχές που κάναμε αρχικά, 
, συνεπώς λύνοντας το παραπάνω σύστημα ως προς 
έχουμε:
, συνεπώς λύνοντας το παραπάνω σύστημα ως προς έχουμε:
Κι εφόσον
τελικά προκύπτει
Δηλαδή, σε αυτήν την περίπτωση το διαστημόπλοιο κερδίζει ταχύτητα ίση με το διπλάσιο της τροχιακής ταχύτητας του πλανήτη!!!
Υπό γωνία αλληλεπίδραση
Ας εξετάσουμε τώρα την περίπτωση που το διαστημόπλοιό μας πλησιάζει έναν πλανήτη υπό γωνία, όπως φαίνεται στην παρακάτω εικόνα. Δεχόμαστε ότι η διεύθυνση κίνησης του πλανήτη είναι ο x-άξονας και η κάθετη σε αυτόν που κείται στο τροχιακό επίπεδο, ο y-άξονας. Το διαστημόπλοιο αρχικά κινείται με ταχύτητα μέτρου 
, η οποία σχηματίζει γωνία θ με την ταχύτητα του πλανήτη.
Αναλύοντας σε συνιστώσες και χρησιμοποιώντας τον ίδιο συμβολισμό όπως και παραπάνω, έχουμε για την αρχική ταχύτητα:
, η οποία σχηματίζει γωνία θ με την ταχύτητα του πλανήτη.
Αναλύοντας σε συνιστώσες και χρησιμοποιώντας τον ίδιο συμβολισμό όπως και παραπάνω, έχουμε για την αρχική ταχύτητα:
και
ενώ για την τελική ταχύτητα:
και
Συνεπώς
και με λίγη μαθηματική επεξεργασία
Όπως εύκολα διαπιστώνουμε, όσο οξύτερη είναι η γωνία αυτή, τόσο μεγαλύτερη η ώθηση του διαστημοπλοίου. Μάλιστα όταν θ=0o, τότε καταλήγουμε στο αποτέλεσμα της μετωπικής αλληλεπίδρασης, δηλαδή
.
Κατ' αναλογία με την βαρυτική σφενδόνη, ένα παιδί ρίχνει
μία μπάλα (που αντιστοιχεί στο διαστημόπλοιο) σε έναν
κινούμενο σιδηρόδρομο (που αντιστοιχεί στον πλανήτη),
Καθώς η μπάλα συγκρούεται με τον σιδηρόδρομο, «δανείζεται»
ένα μέρος από την ορμή του.
Θα πρέπει εδώ να τονιστεί, αν και ίσως είναι περιττό, ότι η αύξηση της ταχύτητας που προκαλεί μια βαρυτική ώθηση, και συνεπώς της Κινητικής Ενέργειας του διαστημοπλοίου, δεν συνεπάγεται καμία παραβίαση της αρχής διατήρησης της ενέργειας, αφού για έναν ηλιοκεντρικό παρατηρητή η αύξηση της Κινητικής Ενέργειας του διαστημοπλοίου ισοφαρίζεται από μια ίση μείωση της Κινητικής Ενέργειας του Πλανήτη, οπότε στο σύστημα διαστημόπλοιο - Πλανήτης, η ενέργεια συνολικά παραμένει σταθερή.
Με την χρήση ενός δικτύου κωνικών τομών και κατάλληλων ελιγμών βαρυτικών ωθήσεων, σε διαφορετικά ενεργειακά επίπεδα, είναι δυνατόν να πλοηγηθεί κάποιος σε ολόκληρο το Ηλιακό Σύστημα.
Xαρακτηριστικό παράδειγμα εφαρμογής των ελιγμών που χρησιμοποιούν βαρυτικές ωθήσεις, είναι η χάραξη της πορείας της «διαστημικής εκστρατείας» στο Ηλιακό μας Σύστημα - και πέρα από αυτό-, των διαστημοπλοίων Voyager 1 και 2.
H διαστρική διαστημική αποστολή τους ξεκίνησε με την εκτόξευση του Voyager 2, στις 20 Αυγούστου 1977, από το Κέντρο Διαστημικών Πτήσεων Kennedy. Ακολούθησε η εκτόξευση του Voyager 1, στις 5 Σεπτεμβρίου, 1977.
Σκοπός της, η επέκταση της εξερεύνησης του Ηλιακού Συστήματος, πέρα από την γειτονιά των εξωτερικών πλανητών, στο όριο επιρροής της Ηλιόσφαιρας και πιθανόν ακόμη παραπέρα. Διασχίζοντας το εξωτερικό Ηλιακό Σύστημα, τα δύο Voyagers αναζητούν το όριο της Ηλιόπαυσης, τα εξωτερικά όρια του Ηλιακού Μαγνητικού Πεδίου και την προς τα έξω ροή του ηλιακού ανέμου.
Με την χρήση ενός δικτύου κωνικών τομών και κατάλληλων ελιγμών βαρυτικών ωθήσεων, σε διαφορετικά ενεργειακά επίπεδα, είναι δυνατόν να πλοηγηθεί κάποιος σε ολόκληρο το Ηλιακό Σύστημα.
Xαρακτηριστικό παράδειγμα εφαρμογής των ελιγμών που χρησιμοποιούν βαρυτικές ωθήσεις, είναι η χάραξη της πορείας της «διαστημικής εκστρατείας» στο Ηλιακό μας Σύστημα - και πέρα από αυτό-, των διαστημοπλοίων Voyager 1 και 2.
H διαστρική διαστημική αποστολή τους ξεκίνησε με την εκτόξευση του Voyager 2, στις 20 Αυγούστου 1977, από το Κέντρο Διαστημικών Πτήσεων Kennedy. Ακολούθησε η εκτόξευση του Voyager 1, στις 5 Σεπτεμβρίου, 1977.
Σκοπός της, η επέκταση της εξερεύνησης του Ηλιακού Συστήματος, πέρα από την γειτονιά των εξωτερικών πλανητών, στο όριο επιρροής της Ηλιόσφαιρας και πιθανόν ακόμη παραπέρα. Διασχίζοντας το εξωτερικό Ηλιακό Σύστημα, τα δύο Voyagers αναζητούν το όριο της Ηλιόπαυσης, τα εξωτερικά όρια του Ηλιακού Μαγνητικού Πεδίου και την προς τα έξω ροή του ηλιακού ανέμου.
Ένας από τους στόχους των Voyagers είναι ο εντοπισμός της Ηλιόπαυσης, της περιοχής εκείνης όπου η επίδραση του Ηλιακού ανέμου πέφτει και μπορεί να ανιχνευτεί ο διαστρικός χώρος.
Πρόσφατα μάλιστα το Voyager 1, έχοντας διασχίσει περίπου 18 δισ. χλμ., εισήλθε σε μια μυστηριώδη περιοχή μετάβασης στα όρια της Ηλιόσφαιρας, την λεγόμενη Ζώνη Εξασθένησης ή Μαγνητική Λεωφόρο, της οποίας την ύπαρξη δεν γνωρίζαμε. Στην περιοχή αυτή, οι γραμμές του Μαγνητικού Πεδίου που παράγεται από τον Ήλιο πυκνώνουν ενώ τα φορτισμένα, χαμηλής ενέργειας σωματίδια που επιταχύνονται στo ταραχώδες εξωτερικό στρώμα της ηλιόσφαιρας εξαφανίζονται. Οι επιστήμονες εκτιμούν ότι αυτή είναι η τελευταία περιοχή της Ηλιόσφαιρας που διασχίζουν τα διαστημόπλοια πριν εξέλθουν στον Διαστρικό Χώρο.
Προσομοίωση των τροχιών των διαστημοπλοίων Voyager I & II προς τους εξωτερικούς πλανήτες του Ηλιακού Συστήματος. Φαίνονται οι χαρακτηριστικές κάμψεις της τροχιάς των σκαφών καθώς περνούν από την γειτονιά των πλανητών.
Στις 18 Οκτωβρίου 1989, ένας άλλος ουράνιος εξερευνητής με το όνομαGalileo, εκτοξεύτηκε με προορισμό τον πλανήτη Δία. Η αποστολή του έληξε όταν βυθίστηκε στην συνθλιπτική ατμόσφαιρα του γιγάντιου πλανήτη στις 21 Σεπτεμβρίου 2003. Η καταστροφή του ήταν σκόπιμη, ώστε να προστατευτεί μία από τις ανακαλύψεις του - ένας πιθανός ωκεανός κάτω από την παγωμένη κρούστα του δορυφόρου Ευρώπη.
Ο Γαλιλαίος άλλαξε τον τρόπο με τον οποίου βλέπουμε το ηλιακό μας σύστημα. Ήταν το πρώτο σκάφος που πέταξε πίσω από έναν αστεροειδή και το πρώτο που ανακάλυψε δορυφόρο σε αστεροειδή και παρείχε άμεσες παρατηρήσεις σύγκρουσης ενός κομήτη με έναν πλανήτη.
Πρώτος πήρε μετρήσεις της ατμόσφαιρας του Δία, με την χρήση ενός καταβατικού ανιχνευτή και πρώτος πραγματοποίησε μακροπρόθεσμες μετρήσεις του πλανήτη. Βρήκε επίσης στοιχεία ύπαρξης αλμυρού νερού κάτω από την Ευρώπη, τον Γανυμήδη και την Καλλιστώ και αποκάλυψε την ένταση της ηφαιστειακής δραστηριότητας στην Ιώ.
Η πορεία του διαστημικού σκάφους Γαλιλαίος.
Μετά την εκτόξευσή του (18 Οκτωβρίου, 1989), πραγματοποίησε τρεις
Μετά την εκτόξευσή του (18 Οκτωβρίου, 1989), πραγματοποίησε τρεις
ελιγμούς, έναν γύρω από την Αφροδίτη, έπειτα γύρω από την Γη
και πάλι την Γη, ώστε να αποκτήσει αρκετή ταχύτητα
για να φτάσει στην τροχιά του Δία.
Ναι μεν... αλλά!
Έχοντας διαβάσει κάποιος την απλουστευμένη σκιαγράφηση του φαινομένου της βαρυτικής σφενδόνης που προηγήθηκε, ίσως αποκομίσει την εντύπωση πως τα πράγματα «εκεί έξω» είναι απλά. Το μόνο που χρειάζεται για μια διαστημική αποστολή είναι ένα καλό και τεχνολογικά εξοπλισμένο διαστημοσκάφος, καύσιμα αρκετά για την εκτόξευση και την αποδέσμευση από το βαρυτικό πεδίο της Γης, και το ακρωτήριο... Κανάβεραλ. Την υπόλοιπη δουλειά την κάνει ο βοηθός της Βαρύτητας που προσφέρεται δωρεάν και απλόχερα στον Μεσοπλανητικό Χώρο του Ηλιακού Συστήματος.Στην πραγματικότητα βέβαια, τα πράγματα είναι... κάπως πιο πολύπλοκα!
H αλήθεια είναι πως οι Χωρικοί και Χρονικοί περιορισμοί στους οποίους υπόκεινται τα διαστημικά μας ταξίδια (εντός ή εκτός του ηλιακού συστήματος) είναι τεράστιοι και δεν είναι καθόλου εύκολο να τους υπερσκελίσει κανείς. Μάλιστα, κάποιος θα πει πως, από ένα σημείο και μετά, δεν είναι καν εφικτό.
Αξιολογώντας από την σκοπιά της ενέργειας τις διαστημικές αποστολές που χαράχθηκαν στην βάση της Ουράνιας Μηχανικής των Kepler και Newton, διαπιστώνει ότι όσο πετυχημένες κι αν ήταν αυτές, παραμένουν κάποια βασικά μειονεκτήματα που περιορίζουν το «βεληνεκές» τους.
Κι αυτό, διότι παρόλο που το μοντέλο σχεδίασης των αποστολών το οποίο βασίζεται στις κωνικές τομές, φαίνεται να λειτουργεί καλά, ο παράγοντας της καύσιμης ύλης που είναι απαραίτητη για την πραγματοποίησή τους, περιορίζει σημαντικά το δρομολόγιο του διαστημοπλοίου, ακόμη και με την αρωγή της βαρυτικής ώθησης.
Για παράδειγμα, χρειάζεται μία σημαντική ποσότητα καυσίμων ώστε ένα σκάφος να «φρενάρει», να τεθεί σε τροχιά γύρω από κάποιον πλανήτη ή δορυφόρο, να παραμείνει εκεί για λίγο και στην συνέχεια να εκτοξευτεί προς τον επόμενο προορισμό.
Συνεπώς, καθώς το μέγεθος ενός σκάφους είναι περιορισμένο, όσο αυξάνεται η ποσότητα του καυσίμου με το οποίο πρέπει να εφοδιαστεί μια αποστολή, τόσο μικραίνει ο επιστημονικός εξοπλισμός που μπορεί να μεταφέρει.
Συνεπώς, καθώς το μέγεθος ενός σκάφους είναι περιορισμένο, όσο αυξάνεται η ποσότητα του καυσίμου με το οποίο πρέπει να εφοδιαστεί μια αποστολή, τόσο μικραίνει ο επιστημονικός εξοπλισμός που μπορεί να μεταφέρει.
Μειώνοντας επομένως την ποσότητα του απαιτούμενου καυσίμου, αυξάνεται η ικανότητα ενός διαστημοσκάφους να μεταφέρει επιστημονικό εξοπλισμό, κάτι που κρίνεται ιδιαίτερα σημαντικό για την εξερεύνηση του διαστήματος.
Εξάλλου, τα περάσματα των διαστημοπλοίων από τους πλανήτες (όπως αυτά των Voyagers) καταλήγουν να είναι πολύ σύντομα (αφού η ταχύτητά τους είναι αρκετά μεγάλη σχετικά με τις πλανητικές ταχύτητες), ώστε το χρονικό διάστημα παρατήρησής τους να είναι ανεπαρκές.
Το επόμενο στάδιο των προσπαθειών επίτευξης της μέγιστης «ενεργειακής οικονομίας» των διαστημικών αποστολών, έχει σημείο εκκίνησης τις προσπάθειες επίλυσης από τον εξέχοντα Γάλλο μαθηματικόJules-Henri Poincaré (1854 – 1912) του προβλήματος των τριών σωμάτων, σταθμούς τα ασταθή Λαγκρανζιανά σημεία, χαοτικά χαρακτηριστικά και αποτέλεσμα την αποκάλυψη ενός δαιδαλώδους ουράνιου δικτύου, της Διαπλανητικής Λεωφόρου.
Το διαστημοσκάφος Cassini-Huygens το οποίο εξερευνά τον Κρόνο.
Από την αρχή της αποστολής του ως σήμερα, οι βαρυτικές ωθήσεις είναι απαραίτητο
στοιχείο της διαδικασίας με την οποία οι επιστήμονες πλοηγούν το σκάφος
στα σημεία που θέλουν να πάει.
Το επόμενο στάδιο των προσπαθειών επίτευξης της μέγιστης «ενεργειακής οικονομίας» των διαστημικών αποστολών, έχει σημείο εκκίνησης τις προσπάθειες επίλυσης από τον εξέχοντα Γάλλο μαθηματικόJules-Henri Poincaré (1854 – 1912) του προβλήματος των τριών σωμάτων, σταθμούς τα ασταθή Λαγκρανζιανά σημεία, χαοτικά χαρακτηριστικά και αποτέλεσμα την αποκάλυψη ενός δαιδαλώδους ουράνιου δικτύου, της Διαπλανητικής Λεωφόρου.
Ομήρου Οδύσσεια, Ραψωδία μ΄, στ. 73-110
Όπου ο Οδυσσέας εξηγεί, πώς κατάφερε να περάσει
μέσα από την Σκύλλα και την Χάρυβδη.
Όπου ο Οδυσσέας εξηγεί, πώς κατάφερε να περάσει
μέσα από την Σκύλλα και την Χάρυβδη.
«‘οἱ δὲ δύω σκόπελοι ὁ μὲν οὐρανὸν εὐρὺν ἱκάνει
ὀξείῃ κορυφῇ, νεφέλη δέ μιν ἀμφιβέβηκε
κυανέη: τὸ μὲν οὔ ποτ᾿ ἐρωεῖ, οὐδέ ποτ᾿ αἴθρη
κείνου ἔχει κορυφὴν οὔτ᾿ ἐν θέρει οὔτ᾿ ἐν ὀπώρῃ.
οὐδέ κεν ἀμβαίη βροτὸς ἀνὴρ οὐδ᾿ ἐπιβαίη,
οὐδ᾿ εἴ οἱ χεῖρές τε ἐείκοσι καὶ πόδες εἶεν:
πέτρη γὰρ λίς ἐστι, περιξεστῇ ἐικυῖα.
μέσσῳ δ᾿ ἐν σκοπέλῳ ἔστι σπέος ἠεροειδές,
πρὸς ζόφον εἰς Ἔρεβος τετραμμένον, ᾗ περ ἂν ὑμεῖς
νῆα παρὰ γλαφυρὴν ἰθύνετε, φαίδιμ᾿ Ὀδυσσεῦ.
οὐδέ κεν ἐκ νηὸς γλαφυρῆς αἰζήιος ἀνὴρ
τόξῳ ὀιστεύσας κοῖλον σπέος εἰσαφίκοιτο.
ἔνθα δ᾿ ἐνὶ Σκύλλη ναίει δεινὸν λελακυῖα.
τῆς ἦ τοι φωνὴ μὲν ὅση σκύλακος νεογιλῆς
γίγνεται, αὐτὴ δ᾿ αὖτε πέλωρ κακόν: οὐδέ κέ τίς μιν
γηθήσειεν ἰδών, οὐδ᾿ εἰ θεὸς ἀντιάσειεν.
τῆς ἦ τοι πόδες εἰσὶ δυώδεκα πάντες ἄωροι,
ἓξ δέ τέ οἱ δειραὶ περιμήκεες, ἐν δὲ ἑκάστῃ
σμερδαλέη κεφαλή, ἐν δὲ τρίστοιχοι ὀδόντες
πυκνοὶ καὶ θαμέες, πλεῖοι μέλανος θανάτοιο.
μέσση μέν τε κατὰ σπείους κοίλοιο δέδυκεν,
ἔξω δ᾿ ἐξίσχει κεφαλὰς δεινοῖο βερέθρου,
αὐτοῦ δ᾿ ἰχθυάᾳ, σκόπελον περιμαιμώωσα,
δελφῖνάς τε κύνας τε, καὶ εἴ ποθι μεῖζον ἕλῃσι
κῆτος, ἃ μυρία βόσκει ἀγάστονος Ἀμφιτρίτη.
τῇ δ᾿ οὔ πώ ποτε ναῦται ἀκήριοι εὐχετόωνται
παρφυγέειν σὺν νηί: φέρει δέ τε κρατὶ ἑκάστῳ
φῶτ᾿ ἐξαρπάξασα νεὸς κυανοπρῴροιο.
«‘τὸν δ᾿ ἕτερον σκόπελον χθαμαλώτερον ὄψει, Ὀδυσσεῦ.
πλησίον ἀλλήλων: καί κεν διοϊστεύσειας.
τῷ δ᾿ ἐν ἐρινεὸς ἔστι μέγας, φύλλοισι τεθηλώς:
τῷ δ᾿ ὑπὸ δῖα Χάρυβδις ἀναρροιβδεῖ μέλαν ὕδωρ.
τρὶς μὲν γάρ τ᾿ ἀνίησιν ἐπ᾿ ἤματι, τρὶς δ᾿ ἀναροιβδεῖ
δεινόν: μὴ σύ γε κεῖθι τύχοις, ὅτε ῥοιβδήσειεν:
οὐ γάρ κεν ῥύσαιτό σ᾿ ὑπὲκ κακοῦ οὐδ᾿ ἐνοσίχθων.
ἀλλὰ μάλα Σκύλλης σκοπέλῳ πεπλημένος ὦκα
νῆα παρὲξ ἐλάαν, ἐπεὶ ἦ πολὺ φέρτερόν ἐστιν
ἓξ ἑτάρους ἐν νηὶ ποθήμεναι ἢ ἅμα πάντας.’[1]
[1]Κείθε θα ιδείς δυο θαλασσόβραχους᾿ του ενός στα ουράνια φτάνει
η σουβλερή κορφή᾿ το σύγνεφο, που εκεί ψηλά τον ζώνει,
το σκοτεινό, κανένας άνεμος δεν το σκορπάει, και μήτε
για καλοκαίρι για χινόπωρο ποτέ η κορφή ξανοίγει.
Θνητός απάνω εκεί δεν πάτησε᾿ κι είκοσι χέρια αν είχε
κι είκοσι πόδια, δε θα δονούνταν ν᾿ ανέβει στην κορφή του᾿
κοφτός ο βράχος ίσια υψώνεται, λες κι είναι δουλεμένος.
Στη μέση εκεί του θαλασσόβραχου, στραμμένη στο σκοτάδι,
στα δυσμικά, μια μαύρη ανοίγεται σπηλιά᾿ και σεις εκείθε
θα προσδιαβείτε λέω με τ᾿ άρμενο, περίλαμπρε Οδυσσέα.
Να ρίξει κι ένας χεροδύναμος θνητός με το δοξάρι
κάτωθε, απ᾿ τ᾿ άρμενο, δε δύνεται να φτάσει στην κουφάλα
του σπήλιου. Μέσα η Σκύλλα κάθεται κι άγρια αλιχτάει᾿ κι αν είναι
σαν κουταβιού μικρού, νιογέννητου το γαύγισμά της, όμως
ατή της άγριο είναι παράλλαμα᾿ θωρώντας τη μπροστά του
κανείς δε θα 'νιώθε αναγάλλιαση, κι αθάνατος αν ήταν.
Έχει μαθές ποδάρια δώδεκα, μισερωμένα, κι έξι
λαιμούς ψηλούς, κι από 'να υψώνεται στις άκρες τους κεφάλι
τρομαχτικό, που ανοιεί το στόμα του με τρεις αράδες δόντια
πυκνά, σφιχτοδεμένα, θάνατο που ξεχειλίζουν μαύρο.
Με το μισό κορμί της κρύβεται στο βαθουλό το σπήλιο,
κι απ᾿ τα φριχτά του βάθη βγάζοντας τις κεφαλές της όξω
ψαρεύει αυτού, στο βράχο ολόγυρα γυρεύοντας δελφίνια,
σκυλόψαρα, για κι αν τρανότερο θεριόψαρο τσακώσει,
από τα μύρια που η βαριόμουγκρη θεά Αμφιτρίτη βόσκει.
Δε βρίσκεται άρμενο που οι ναύτες του να παινευτούν πως φύγαν
από το πλοίο το γαλαζόπλωρο και το τραβάει μαζί του.
Ο άλλος ωστόσο θαλασσόβραχος τόσο αψηλός δεν είναι
κι ουδέ μακριά απ᾿ τον πρώτο᾿ αν έριχνες, τον έφτανε η σαγίτα.
Μια αγριοσυκιά κει πέρα βρίσκεται μεγάλη, φυλλωμένη,
κι η Χάρυβδη η θεϊκιά στη ρίζα της αναρουφάει το κύμα.
Τρεις το ξερνάει κάθε μερόνυχτο φορές και τρεις βρουχιώντας
το αναρουφάει᾿ να μη σου τύχαινε να 'σαι, ως ρουφάει, κοντά της,
τι απ᾿ το χαμό δε θα σε γλίτωνε μηδέ κι ο Κοσμοσείστης!
Γι᾿ αυτό στης Σκύλλας κοντοζύγωσε το βράχο το καράβι
και πέρνα γρήγορα᾿ καλύτερα πολύ από τ᾿ άρμενό σου
να λείψουν έξι μόνο σύντροφοι παρά να λείψουν όλοι.᾿
Παραπομπή : Science Wiki
Πηγή:cqq-am.blogspot.gr
